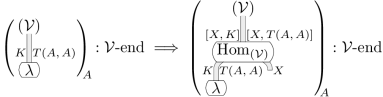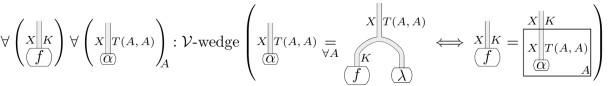Enriched end

以下、

symmetric closed monoidal category: $\mathcal{V} = (\mathcal{V} _ 0, \otimes, I)$
$\mathcal{V}$ -functor: $T : \mathcal{A} ^ {\operatorname{op}} \otimes \mathcal{A} \to (\mathcal{V})$

において･･･

$\mathcal{V}$ -extranatural な $(\alpha _ A : X \to T(A,A) ) _ A$ を

と呼ぶことにする。

$\mathcal{V}$ -wedge to $T$ を 0-cell とする 1-category:

を定義できる。

Hom functor と同様にして 1-functor:

$\operatorname{ \mathcal{V}\mathrm{-wedge} }(\unicode{0x2013}, T) : \mathcal{V} _ 0 ^ {\operatorname{op}} \to \mathcal{Set}$

を定義できる。

上記の category の terminal object:

のことを ending $\mathcal{V}$ -wedge あるいは単に $\mathcal{V}$ -end という(ことにする)*1:

特にこの $K$ を

と書く。

Enriched end は $X$ についての 1-natural bijeciton:

でも表せる(と思う)。

フツーの End - PS と同様に enriched end もまた mono 性を持つ:

f:id:mbps:20150424061230p:plain

代わりに Preservation of ends - PS を参照。

任意の $X$ について $\operatorname{Hom} _ {(\mathcal{V})}(X,\unicode{0x2013})$ preserves ends:

f:id:mbps:20150422162422p:plain

*1:unend と呼んだ方がいいかもしれない

*2:実際は self-"un"riched な形の方が描きやすい