PS

Enriched Yoneda embedding

圏論命題 Enriched Yoneda

Curry isomorphism

以下、Exponentiation 2-functor on enriched categories - PS の補題の isomorphic 1-functor:

$\operatorname{\mathcal{V-}\mathbf{CAT}}(\mathcal{C}, [ \mathcal{A},\mathcal{B} ] ) \cong \operatorname{\mathcal{V-}\mathbf{CAT}}(\mathcal{C} \otimes \mathcal{A},\mathcal{B})$

を使用する。

Enriched fully-faithful functor

$\mathcal{V} _ 0$ -isomorphism の族になっている $\mathcal{V}$ -functor のこと。

Enriched Yoneda embedding

$Y := \tilde{\operatorname{Hom}_{\mathcal{A}}} : \mathcal{A} ^ {\operatorname{op}} \to [\mathcal{A},(\mathcal{V})]$

f:id:mbps:20150513072610p:plain

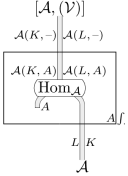
これは Yoneda isomorphism:

$\mathcal{A}(L,K) \cong [\mathcal{A},(\mathcal{V})](\mathcal{A}(K,\unicode{0x2013}),\mathcal{A}(L,\unicode{0x2013}) )$

そのものであるので $Y$ は fully-faithful。

命題

$\mathcal{V}$ -functor:

$P : \mathcal{C} \otimes \mathcal{A} \to \mathcal{B}$
$Q : \mathcal{D} \otimes \mathcal{A} \to \mathcal{B}$

について、Enriched end functor - PS の命題により定まる

$H : \mathcal{C} ^ {\operatorname{op}} \otimes \mathcal{D} \to (\mathcal{V})$
$H(C,D) = [\mathcal{A},\mathcal{B}](P(C,\unicode{0x2013}),Q(D,\unicode{0x2013})) := \displaystyle\int _ A \mathcal{B}(P(C,A),Q(D,A))$

なる $\mathcal{V}$ -functor の実装は次のようになる:

f:id:mbps:20150513081822p:plain

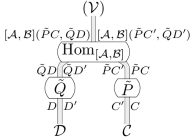
証明

$H$ の一意性による。

系.1

特に

$P := Q := E : [ \mathcal{A},\mathcal{B} ] \otimes \mathcal{A} \to \mathcal{B}$ *1

とすれば、 $1 _ { [ \mathcal{A},\mathcal{B} ] } = \tilde{E}$ なので

- $\mathcal{V}$ -natural in $S, T$

つまり、 $[ \mathcal{A},\mathcal{B} ](S,T)$ という表記に矛盾がない。

系.2

特に

$P := \operatorname{Hom} _ {\mathcal{A}} : \mathcal{A} ^ {\operatorname{op}} \otimes \mathcal{A} \to (\mathcal{V})$
$Q := E : [ \mathcal{A},(\mathcal{V}) ] \otimes \mathcal{A} \to (\mathcal{V})$

とすれば

- $\mathcal{V}$ -natural in $K, F$

参考文献

Basic Concepts of Enriched Category Theory (2.3, 2.4)

*1:Enriched evaluation functor - PS