PS

Enriched hom functor

圏論定義 Enriched

(あるいは hom enriched functor かも)

Enriched difunctor

$T: \mathcal{A} ^ {\operatorname{op}} \otimes \mathcal{A} \to \mathcal{B}$

なる形の $\mathcal{V}$ -bifunctor のこと(を個人的に)。

Enriched hom difunctor

closed symmetric monoidal category: $\mathcal{V} = (\mathcal{V} _ 0, \otimes, I)$
$\mathcal{V}$ -category: $\mathcal{A}$

について、hom $\mathcal{V}$ -difunctor:

$\operatorname{Hom} _ {\mathcal{A}} : \mathcal{A} ^ {\operatorname{op}} \otimes \mathcal{A} \to (\mathcal{V})$ *1

を次のように定義できる:

f:id:mbps:20150404185542p:plain

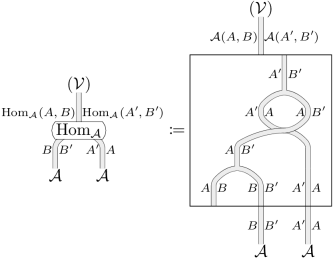
Underlying 1-difunctor of enriched hom functors

$\operatorname{Hom} _ {\mathcal{A}}$ の underlying difunctor:

$\operatorname{hom} _ {\mathcal{A}} : \mathcal{A} ^ {\operatorname{op}} _ 0 \times \mathcal{A} _ 0 \to (\mathcal{V}) _ 0 \overset{\square}{\cong} \mathcal{V} _ 0$

を次のように定義できる:

f:id:mbps:20150404194739p:plain

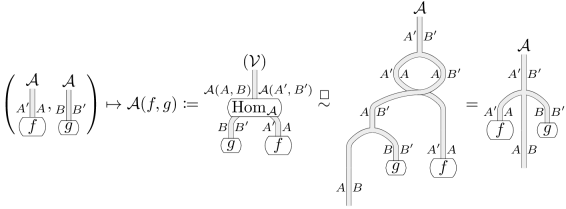
命題

$V := \operatorname{Hom} _{\mathcal{V} _ 0}(I, \unicode{0x2013}) : \mathcal{V} _ 0 \to \mathcal{Set}$ *2

f:id:mbps:20150325213421p:plain

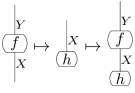
とすると

$\operatorname{Hom} _ { \mathcal{A} _ 0 } = V \circ \operatorname{hom} _ {\mathcal{A}} : \mathcal{A} ^ {\operatorname{op}} _ 0 \times \mathcal{A} _ 0 \to \mathcal{Set}$

参考文献

Basic Concepts of Enriched Category Theory

*1:Self-enriched category - PS

*2:普通の hom functor