PS

Self-enriching

圏論 定義 Enriched

(と呼んでいい気がする)

Self-enriching

Closed symmetric monoidal category:

  • \mathcal{V} := (\mathcal{V} _ 0, \otimes, I)

について、Self-enriched category - PS の命題.1により

  • \mathcal{V} _ 0 \overset{\square}{\cong} (\mathcal{V}) _ 0

f:id:mbps:20150404073330p:plain

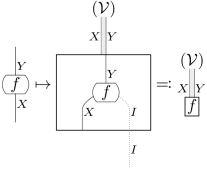
となるのであったが、特にこの currying を self-enriching と勝手に呼ぶことにする。

Functoriality of self-enriching

f:id:mbps:20150404073406p:plain

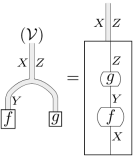
命題

Full and faithful functor - PS により isomorphism は fully faithful であったから、特に

  • \mathcal{V}-category: \mathcal{A}
  • \mathcal{A}-object: B, K

について、self-enriching により

  • \mathcal{A} _ 0 (B, K) = \mathcal{V} _ 0(I, \mathcal{A}(B,K) ) \overset{\square}{\cong} (\mathcal{V}) _ 0 (I, \mathcal{A}(B,K) )

Associated self-enriched naturality

例えば、 \mathcal{V} _ 0-morphism の族:

f:id:mbps:20150404073512p:plain

を self-enrich すると

f:id:mbps:20150404073517p:plain

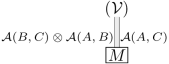
となるが、その \mathcal{V}-naturality は

f:id:mbps:20150404073521p:plain

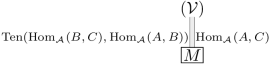
とみなすことで定義できる。

参考文献