PS

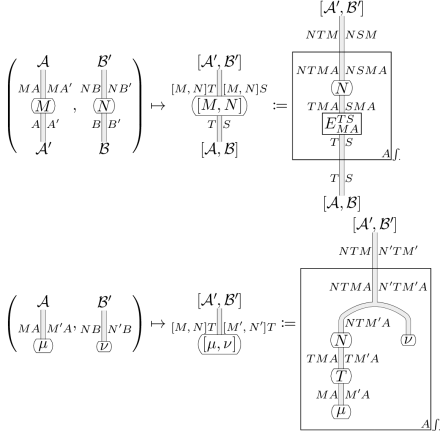
Exponentiation 2-functor on enriched categories

圏論 定義 Enriched

(と呼ぶくらいしか思いつかない)

補題: Close(curry) isomorphisms

f:id:mbps:20150509103836p:plain

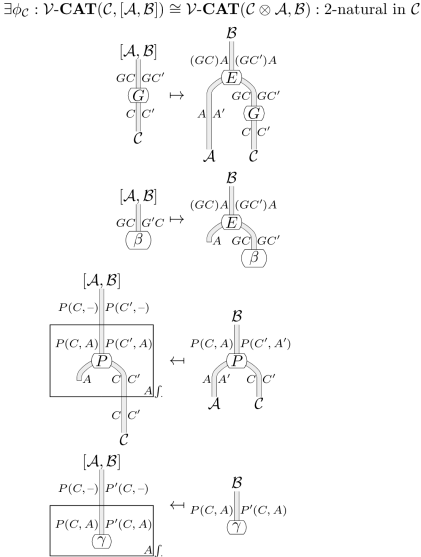
命題

Evaluation \mathcal{V}-functor の族:

  • \big(E _ {\mathcal{A},\mathcal{B}} : [\mathcal{A}, \mathcal{B} ] \otimes \mathcal{A} \to \mathcal{B} \big) _ {\mathcal{A},\mathcal{B} \in \operatorname{\mathcal{V-}\mathbf{CAT}}}

は 2-functor:

  • [-,= ] : \operatorname{\mathcal{V-}\mathbf{CAT}} ^ {\operatorname{op}} \times \operatorname{\mathcal{V-}\mathbf{CAT}} \to _ 2 \operatorname{\mathcal{V-}\mathbf{CAT}}

を create する。

証明

Yoneda bijection により

  • E _ {\mathcal{A,B}} : [ \mathcal{A},\mathcal{B} ] \otimes \mathcal{A} {\to} \mathcal{B}
    • \sim \phi : \operatorname{\mathcal{V-}\mathbf{CAT}}(\unicode{0x2013}, [\mathcal{A},\mathcal{B} ] ) \cong _ 2 \operatorname{\mathcal{V-}\mathbf{CAT}}(\unicode{0x2013} \otimes \mathcal{A}, \mathcal{B} )

となるが、 \mathcal{A,B} についての \mathcal{Cat}-naturality つまり 2-naturality は preserve される*1ので、あとは Enriched representability - PS の命題より。

[-,=] の実装は以下のようになる:

f:id:mbps:20150627193814p:plain

参考文献

*1:Preservation of enriched natural-lookingness - PS