PS

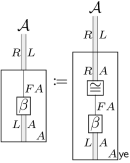
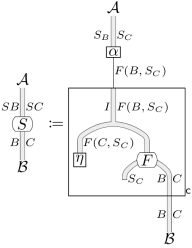
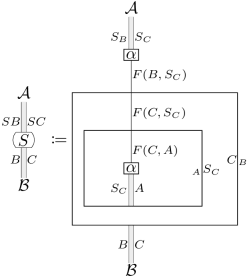
Enriched representability

圏論命題 Enriched

Symmetric closed monoidal category $\mathcal{V}$ において･･･

Enriched representation

$\mathcal{V}$ -functor:

$F : \mathcal{A} \to (\mathcal{V})$

について、 $\mathcal{V}$ -natural isomorphism:

$\mathcal{A}(R,\unicode{0x2013}) \cong F$

なる $(R, \cong)$ を representation of $F$ という。*1

Unit

Representation は Enriched Yoneda lemma (weak form) - PS により

$\eta : I \to FR$ (unit of the representation)

に対応する。

Dual

Dual として corepresentation が定義できるが、特に区別せず representation と呼んでしまうようだ。ただし、unit の dual である counit という用語はよく使われる。

Mediating bijection

f:id:mbps:20150602230211p:plain *2

f:id:mbps:20150602230215p:plain

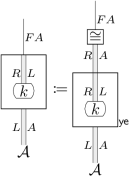
Enriched Yoneda principle (weak form) - PS により、この bijection は iso を preserve する。特に representation は unique up to iso。

命題

$\mathcal{V}$ -functor:

$F : \mathcal{B} ^ {\mathrm{op}} \otimes \mathcal{A} \to (\mathcal{V})$

について、representation of $F(B,\unicode{0x2013})$ の族:

$\big( \alpha ^ B: \mathcal{A}(S _ B,\unicode{0x2013}) \cong F(B,\unicode{0x2013}) \big) _ B$

が存在するならば

$SB = S _ B$
$S$ は unit-compatible
$\alpha ^ B$ は $B$ について $\mathcal{V}$ -natural-looking

なる $\mathcal{V}$ -infrafunctor:

$S : \mathcal{B} \to \mathcal{A}$

がただ一つ存在し、しかも $\mathcal{V}$ -functorial。

証明

f:id:mbps:20150530161605p:plain *3

f:id:mbps:20150530161659p:plain *4

とすると、 $S$ は unit-compatible となるので $\eta$ は $B$ について $\mathcal{V}$ -natural looking。Preservation of enriched natural-lookingness - PS により $\alpha$ および $\mathsf{c}$ 部も $B$ について $\mathcal{V}$ -natural looking。ゆえに Enriched natural-lookingness - PS の命題により左辺は composition-compatible。

証明 @error

参考文献

Basic Concepts of Enriched Category Theory 1.10

*1:一般に enriched universal morphism 的なものはないらしい

*2:Yoneda embedding bijection

*3:Yoneda bijection

*4:curry bijection