PS

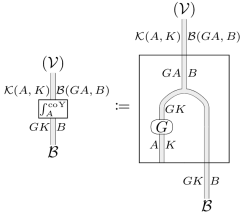
Weighted colimit

圏論 定義 命題 Enriched Weighted limit

Opposite category の記法 @deprecated

  • A ^ {\ast} \in \mathcal{A} ^ {\operatorname{op}} \iff A \in \mathcal{A}

とすると

  1. A ^ {\ast \ast} = A
    • (\mathcal{A} ^ {\operatorname{op}})^ {\operatorname{op}} = \mathcal{A}
  2. F ^ {\operatorname{op}} A ^ {\ast} = (FA) ^ {\ast}
  3. (A ^ {\ast}, B ^ {\ast}) = (A, B) ^ {\ast}
    • \mathcal{A} ^ {\operatorname{op}} \otimes \mathcal{B} ^ {\operatorname{op}} = (\mathcal{A} \otimes \mathcal{B} ) ^ {\operatorname{op}}
  4. F ^ {\ast} \sim F ^ {\operatorname{op}}
    • \lbrack \mathcal{A}, \mathcal{B} \rbrack ^ {\operatorname{op}} \cong \lbrack \mathcal{A} ^ {\operatorname{op}}, \mathcal{B} ^ {\operatorname{op}} \rbrack

A \mapsto A ^ {\ast} は functorial にならないことに注意する。

以下、この記法により variance を明示する。

Weighted limit @deprecated

  • \lbrace F ^ \ast, G \rbrace : \mathcal{B}
  • \displaystyle\lim _ K {} ^ {F ^ \ast} GK {}
  • \mathcal{B}(B ^ {\ast},\lbrace F ^ {\ast}, G \rbrace) \cong \lbrack \mathcal{K}, (\mathcal{V}) \rbrack (F ^ {\ast}, K \mapsto \mathcal{B}(B ^ {\ast}, GK) )
    • F : \mathcal{K} \to (\mathcal{V})
    • G: \mathcal{K} \to \mathcal{B}

Weighted colimit @deprecated

  • F \star G := \lbrace F ^ {\ast}, G ^ {\operatorname{op}} \rbrace ^ {\ast} : \mathcal{B}
  • \underset{K}{\operatorname{colim}} {} ^ F GK := ( \displaystyle\lim _ {K ^ \ast} {} ^ {F ^ \ast} (GK) ^ \ast ) ^ \ast
  • \mathcal{B}( (F \star G) ^ {\ast} , B) \cong \lbrack \mathcal{K} ^ {\operatorname{op}}, (\mathcal{V}) \rbrack (F ^ {\ast}, K ^ {\ast} \mapsto \mathcal{B}(G^ {\operatorname{op}}K ^ {\ast}, B) )
    • F : \mathcal{K} ^ {\operatorname{op}} \to (\mathcal{V})
    • G : \mathcal{K} \to \mathcal{B}

Commutativity Symmetricity of weighted colimits

  • \operatorname{colim} _ K ^ {FK} GK \cong \operatorname{coliim} _ K ^ {GK} FK
    • F : \mathcal{K} ^ {\operatorname{op}} \to (\mathcal{V})
    • G : \mathcal{K} \to (\mathcal{V})

証明

f:id:mbps:20150825115538p:plain

証明 @deprecated

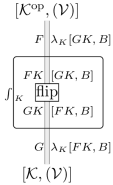
@deprecated

Yoneda lemma via weighted limits

  • \operatorname{lim} _ A ^ { \mathcal{K}(K,A) } GA \cong GK
    • G : \mathcal{K} \to \mathcal{B}

Yoneda lemma via weighted colimits (co-Yoneda lemma)

  • \operatorname{colimi} _ A ^ {\mathcal{K}(A,K)} GA \cong GK
    • G : \mathcal{K} \to \mathcal{B}

f:id:mbps:20150828015803p:plain

証明 @deprecated

@deprecated

参考文献